Le principe est que tout système semble évoluer d'un état à un autre toujours en utilisant les moyens les plus simples et en conservant une grandeur constante entre les deux états:
Les moyens en question peuvent être: le chemin le plus court, le chemin le plus rapide (les trajectoires spatio-temporelles à plus faibles amplitudes...)
Selon le premier principe fondamental de la physique, la grandeur constante est choisie comme étant l'énergie
Cet énoncé est appelé dans le cadre de la mécanique "principe de moindre action (de Maupertuis)" ou dans le cadre de la physique générale "principe variationnel" ou encore parfois dans le cadre de l'optique "principe d'économie" ou "principe de Fermat". Dans le cadre mathématique faisant purement abstraction des concepts physiques, nous parlons de "principe de Hamilton".
Plus techniquement, il est aussi formulé de la manière suivante: Un système se meut d'une configuration à une autre de telle façon que la variation de l'action (voir plus loin) entre la trajectoire naturelle effectivement suivie et toute trajectoire virtuelle infiniment voisine ayant les mêmes extrémités dans l'espace et dans le temps soit nulle. Autrement dit, parmi tous les chemins possibles entre deux points donnés de l’espace, la trajectoire physique (réelle) d’un objet est le chemin qui minimise (ou en général “extrémise”) une certaine quantité définie sur toute la trajectoire, appelée action.
La mécanique analytique, initiée dès le 18ème siècle, regroupe ainsi différentes formulations très mathématisées de la mécanique classique, notamment les mécaniques de Hamilton et de Lagrange (Formulations sont équivalentes).
Cette formalisation est assez peu enseignée dans les petites écoles car il faut bien reconnaître que le formalisme lagrangien et hamiltonien (contenant donc le principe de moindre action sous forme mathématique) fait appel à un niveau d'abstraction un peu plus élevé que les méthodes normales et malgré qu'il soit souvent d'une aide précieuse dans l'élaboration de théories (physique fondamentale, physique quantique, relativité générale, théorie quantique des champs, théorie des supercordes), il en découle rarement de nouvelles solutions (mais plutôt une réduction et une méthode de validation utile et très puissante).
1. COORDONNÉES GÉNÉRALISÉES ET RÉFÉRENTIELS
Un réflexe naturel conduit généralement à référer la position d'un point dans l'espace à la seule connaissance de ses trois coordonnées cartésiennes x, y, z. Cette attitude est d'ailleurs le plus souvent justifiée par la simplicité d'un grand nombre de situations rencontrées dans la pratique, où il n'est pas nécessaire de rechercher de méthodes plus élaborées ou de passer dans d'autres systèmes de coordonnées (cf. section de Calcul Vectoriel).
Pour repérer la position d'un mobile (ou d'un point matériel) en physique il est nécessaire dans un premier temps d'associer un repère au référentiel. Ainsi, un "repère" est un système (physique concret) de repérage dans l'espace associé au référentiel.
Les repères conventionnels en mécanique classique constituent majoritairement des bases d'espaces pré-euclidiens canoniques (cf. chapitre de Calcul Vectoriel) orientés et où chaque point, ou vecteur de l'espace, peut-être représenté algébriquement par ses valeurs d'affixes (la valeur à l'ordonnée (projection sur l'axe vertical) et la valeur à l'abscisse (projection sur l'axe horizontal).
Voici quelques exemples :

Définitions:
Un repère, assimilé à un référentiel, est dit "référentiel Galiléen" (c'est rare que nous en fassions explicitement mention en physique par manque de rigueur) si:
- Nous pouvons le considérer comme immobile pendant toute l'étude du mouvement du système ou comme étant en translation rectiligne uniforme par rapport à un autre référentiel lui-même immobile. Donc si nous négligeons le mouvement de rotation du Soleil autour du centre de la galaxie, alors le référentiel héliocentrique peut être considéré comme galiléen. Si nous négligeons le mouvement de rotation de la Terre autour du Soleil, alors le référentiel géocentrique peut être considéré comme galiléen. Si nous négligeons le mouvement de rotation de la Terre sur elle-même, alors le référentiel terrestre peut être considéré comme galiléen. Dans beaucoup d'expériences de mécanique à la surface de la Terre, nous constatons que le référentiel terrestre peut être considéré comme galiléen avec une très bonne précision.
- Nous pouvons le considérer comme un système où les lois de Newton sont vérifiées
Un repère, assimilé à un référentiel, est dit "barycentrique"s'il a pour origine le centre de masse du corps étudié. Ainsi, le "repère de Copernic" est assimilé au centre de gravité (d'inertie) du système solaire, le "repère héliocentrique" appelé aussi "repère de Kepler" au centre d'inertie du Soleil.
Un repère, assimilé à un référentiel, est dit "référentiel géocentrique" lorsque nous prenons pour référence un système d'axes placés au centre d'inertie de la Terre. Les axes, parallèles à ceux du référentiel de Copernic, pointent vers trois étoiles fixes. Dans ce référentiel la Terre tourne sur elle-même en 24h.
Un repère, assimilé à un référentiel, est dit "référentiel Terrestre" lorsque nous prenons pour référence un système d'axes placés au centre d'inertie de la Terre et qui a un mouvement de rotation uniforme correspondant à la vitesse de rotation de la Terre. Traditionnellement un des axes est dirigé vers l'étoile polaire. C'est le référentiel auquel nous nous référons le plus dans la vie courante il n'est donc pas galiléen en toute rigueur! Ceci va induire des effets particuliers sur les mouvements dans l'atmosphère tels que nous les ressentons.
Il est bien exact que les trois paramètres x, y, z suffisent parfaitement à repérer un point matériel dans l'espace usuel comme nous en avons déjà fait mention dans notre étude des espaces ponctuels (cf. chapitre sur les Principes), mais il n'en demeure pas moins qu'il est parfois inévitable, ou même tout simplement plus avantageux, d'utiliser un nombre de paramètres supérieur à trois. Nous pouvons évidemment envisager toutes sortes de paramétrages pour atteindre les coordonnées d'un point dans l'espace, de telle sorte que, d'une façon plus généralisée nous serons amenés à prendre en considération des relations du type (nous ne gardons plus la même écriture que celle que nous avions lors de notre étude des espaces ponctuels par cohérence avec les nombreuses références déjà existant sur le sujet):

Les paramètres q1,q2,...,qn portent le nom de "coordonnées généralisées", paramètres auxquels un problème sera le plus souvent référé. Connaître leur expression en fonction du temps est le problème fondamental de la dynamique. Cela signifie que nous serons parvenus à une solution quand nous disposerons des relations indépendantes:

Il est donc important de retenir que le nombre de paramètres qi définissant le repérage d'un point dans l'espace est au moins égal à trois, sans être nécessairement différent de trois. C'est finalement la nature des situations envisagées qui suggèrent le choix du nombre des paramètres à utiliser (coordonnées cartésiennes, cylindriques, sphériques,...).
Dans une vision plus générale, la configuration instantanée d'un système, quelle qu'en soit la nature, sera déterminée par la connaissance, en fonction du temps, de n paramètres, n définissant le nombre de "degrés de liberté" du système.
Il est normal, mathématiquement, d'associer la manipulation des n paramètres xi au recours à un hyper-espace à n dimensions, dans lequel les xi apparaîtraient comme les coordonnées d'un point P représentatif de la configuration d'un système quelconque. Nous donnons à cet espace à n dimensions En, le nom "d'espace de configuration".
Mais la rigueur de la mathématique-physique, nous amène à disposer d'une description plus précise des phénomènes en ajoutant cette variable importante qu'est le temps, considérée souvent comme variable indépendante, aux xi . Nous en arriverons donc fatalement à utiliser un autre hyper-espace En+1 auquel nous avons donné le nom "d'espace des événements".
Ce dernier espace de référence revêt un intérêt capital pour un grand nombre de problèmes de la science moderne et se trouve particulièrement bien adapté aux raisonnements de nature relativiste. Les variables indépendantes constituant les coordonnées spatiales et temporelles forment alors ce que nous appelons les "variables d'Euler".
Dans la mesure où les paramètres xi sont simplement présentés comme des fonctions explicites du temps, le point P décrit une courbe paramétrée, définie par xi = xi(t) , avec i=1,2....,n . Cela revient à exploiter simultanément les équations:

Il arrivera fréquemment que, pour des raisons d'opportunité, nous souhaitions changer de système de coordonnées généralisées, et utiliser un autre ensemble plus compatible avec les spécificités du problème envisagé. Nous substituerons alors au jeu des xi un nouveau jeu de coordonnées qi. Il est alors évident que nous devrons, avant toute chose, nous doter des relations de dépendance existant entre les deux ensembles de coordonnées (cf. section de Calcul Vectoriel):

Dans ces conditions, à chaque point Px de l'espace des configurations des x, noté Ex, correspondra un point Pq de l'espace de configuration des q, noté Eq. Nous avons ainsi effectué une transformation ponctuelle, autrement dit une application de l'espace sur lui-même.
Pour étudier des milieux continus (concept différent du point matériel), nous aurons cependant deux approches différentes:
1. Méthode de Lagrange: nous cherchons à caractériser le mouvement du milieu décrit par une formulation Lagrangienne consistant donc à le caractériser en se donnant un système d'équations au sens newtonien. Par dérivations, nous avons alors la vitesse et l'accélération du milieu.
2. Méthode d'Euler: Au lieu de suivre le parcours d'un point, nous portons notre attention sur l'évolution des caractéristiques physiques en un point donné comme la vitesse, l'accélération, la température, la pression ou autre. Nous parlons alors fréquemment de "système Eulérien".
1.1. PRINCIPE VARIATIONNEL
Selon l'énoncé du principe variationnel nous devons trouver dans tout phénomène
physique, une certaine quantité qui est naturellement optimisée (minimisée ou maximisée) et qui décrit toutes les variables du système étudié et ainsi son issue.
Voici la démarche que nous allons suivre:
1) Nous supposons donc le principe variationnel et le principe de conservation de l'énergie comme justes.
2) L'énergie totale d'un système fermé est constante et constituée de la sommation de l'énergie cinétique et l'énergie potentielle.
3) Si nous ne considérons que l'énergie cinétique, alors le système est dit "système libre"; si les deux énergies sont considérées, nous disons alors que le système est un "système généralisé".
4) Nous définissons une fonction mathématique (dont les variables sont les coordonnées généralisées) appelée "Lagrangien" qui est donnée par la différence entre les deux énergies précitées. Dans le cadre de la mécanique lagrangienne, la densité lagrangienne est une quantité mathématique qui représente la densité d'énergie d’un système / particule en mouvement. Elle est généralement définie comme la différence entre l'énergie potentielle et cinétique du système.
NB : L'énergie cinétique décrit l'énergie d'un système associée à son mouvement (1/2mv2), tandis que l'énergie potentielle décrit l'énergie d'un système associée à sa position ou configuration. L'énergie potentielle est déterminée par les forces extérieures agissant sur la particule et peut être exprimée comme une fonction U(x) où x représente la position de la particule (mv). Considérons l'exemple d'un objet tombant en chute libre, son énergie cinétique augmente progressivement à mesure qu'il tombe vers le sol. Cela est dû à la conversion de son énergie potentielle gravitationnelle en énergie cinétique
En effet, au départ, l'objet a de l'énergie potentielle gravitationnelle en raison de sa hauteur par rapport au sol. Lorsqu'il commence à tomber, cette énergie potentielle gravitationnelle est convertie en énergie cinétique. Plus l'objet tombe, plus sa vitesse augmente, et donc plus son énergie cinétique augmente. Cependant, il est important de noter que la somme de l'énergie cinétique et de l'énergie potentielle de l'objet reste constante, selon le principe de conservation de l'énergie. Ainsi, bien que l'énergie cinétique augmente, l'énergie potentielle gravitationnelle diminue de manière équivalente. Lorsque l'objet atteint le sol, toute son énergie potentielle gravitationnelle a été convertie en énergie cinétique. À ce moment, son énergie cinétique est à son maximum, mais son énergie potentielle gravitationnelle est à zéro. La somme totale de l'énergie cinétique et de l'énergie potentielle gravitationnelle de l'objet est alors égale à son énergie mécanique totale, qui est conservée tout au long de la chute libre.
5) Sur l'évolution d'un système entre deux états, nous cherchons les propriétés de la fonction (du lagrangien) qui donne la minimisation de la variation de la différence des deux énergies sur l'évolution temporelle ou métrique du système.
Enfin, une fois cette propriété déterminée (mise sous la forme que nous appelons "équation d'Euler-Lagrange") nous chercherons toutes les autres propriétés possibles afin d'avoir les outils nécessaires pour la physique théorique.
Donc, pour mettre cela sous forme mathématique, nous commençons par poser qu'il existe une fonction réelle de 2n variables:

que nous appellerons "Lagrangien généralisé" du système, dont l'intégrale satisfait à l'énoncé suivant:
Dans un mouvement naturel partant d'un point
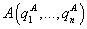
à l'instant tA, arrivant au point
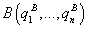
à l'instant tB, l'intégrale suivante appelée "intégrale d'action" ou simplement "action":

qui peut aussi être notée dans une écriture plus abrégée:

doit être un extrémum (en fait, "un minimum" ou "un maximum", puisque nous aurions pu tout aussi bien prendre -L au lieu de +L dans le choix de la définition du Lagrangien généralisé).
L'action S est ce que nous appelons communément en physique une "fonctionnelle" constitue une unité d'énergie multipliée par le temps puisque L est une énergie.
1.2. ÉQUATION D'EULER-LAGRANGE
Le principe de moindre action énonce donc que l'action S est extrêmale si:

représentant la trajectoire d'un point masse au cours du temps est une trajectoire naturelle effectivement suivie par le système physique (les paramètres qi permettent de définir le repèrage du point dans l'espace).
Considérons alors une trajectoire très voisine à la précédente, que nous noterons:

C'est-à-dire que pour chaque i nous posons:

avec:

pour assurer que nous partons toujours du même point A pour arriver au même point :

Si S(q,q.) est bien l'évolution d'un système évoluant selon le principe de moindre action, alors l'action donnée par la variation:

est nulle pour δq et δq. tendant vers zéro (sous-entendu que tout système physique revient à son état initial sans intervention extérieure).
Soit:

Ce qui nous permet de justifier la dénomination de "principe variationnel" (aussi appelé parfois le "principe de stationnarité de l'action"):

Ce principe stipule donc que la trajectoire d'une particule (ou d'un système de manière plus générale) s'obtient en demandant qu'une certaine fonctionnelle S appelée "action" soit stationnaire par rapport à une variation de la trajectoire. En d'autres termes, si nous effectuons une variation infiniment petite de la trajectoire, la variation doit être nulle.
Pour un système mécanique simple, l'action est alors évidemment, de par le principe de conservation de l'énergie égale à l'intégrale sur la trajectoire de (par définition du lagrangien) la différence entre l'énergie cinétique et l'énergie potentielle.
Dès lors, dans une théorie pour laquelle les forces dérivent d'un potentiel V, nous sommes naturellement amenés à définir le "Lagrangien" par la relation (il faudra s'en souvenir):

où T et V sont la notation traditionnelle dans le formalisme Lagrangien de l'énergie cinétique et de l'énergie potentielle données par:
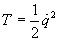
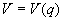
NB: Pour l'étude de la relativité générale, nous ne chercherons pas à ce que la variation de la différence des énergies soit minimale tel que c'est le cas pour les systèmes mécaniques, mais bien la variation de la longueur d'un arc ds (non dépendant du temps contrairement à l'exemple précédent) dans un espace quelconque lors d'une trajectoire d'un système libre. Ce qui nous amènera à écrire simplement (rappelez-vous en aussi car ce sera très important) l'action:

pour une masse unitaire et en prenant les unités naturelles.
Pour revenir à notre application du principe variationnel dans le cas du lagrangien généralisé, nous pouvons alors écrire la différentielle totale exacte de dL et nous obtenons alors la relation:

Intégrons par parties le deuxième terme de la somme de l'intégrale précédente:

Le premier terme de la dernière égalité est nul puisque nous avons déjà mentionné plus haut que par construction :

Donc:

L'expression de l'intégrale de moindre action peut finalement s'écrire :

Mais les δq et δq. tendant vers zéro d'une infinité de manières différentes (sous-entendu que tout système physique revient à son état initial sans intervention extérieure), nous devons cependant avoir δS = 0. Cela veut dire alors que chaque terme sommé de l'intégrale peut être pris indépendamment et doit satisfaire:

Mais comme les fonctions δq et δq. peuvent toujours tendre vers zéro de multiples façons, et que cette intégrale doit être quand même nulle, nous en déduisons que ce sont les intégrandes qui sont nuls:

Ces n équations, satisfaites par le lagrangien généralisé du système pour le mouvement effectivement suivi, sont appelées "équations d'Euler-Lagrange", ou "équations de Lagrange". Ce sont, comme nous allons le voir, les équations du mouvement du système résolues, elles donnent l'évolution effective du système dans le temps:

Donc dans l'approche lagrangienne, nous apprenons à raisonner à partir des concepts d'énergie potentielle et cinétique, au lieu des concepts de force. Les deux approches sont évidemment équivalentes physiquement, mais les énergies n'étant pas des quantités vectorielles, elles sont conceptuellement plus faciles à utiliser dans une vaste gamme de problèmes. En physique quantique par exemple, la notion de force n'a aucune signification mais les notions d'énergie demeurent valables. C'est une raison de plus pour se familiariser avec leur utilisation. De plus, la force au sens de Newton est une action instantanée à distance. En relativité, une telle chose est impossible. La notion de force est donc une création purement classique et macroscopique.
Considérons un exemple d'application particulièrement trivial de l'équation d'Euler-Lagrange. Il consiste à déterminer le plus court chemin entre deux points A et B d'un plan (évidemment une droite mais il faut le démontrer!) :

En notant s l’abscisse curviligne le long d’un chemin, on a:

Posons sous une forme mathématique conventionnelle l'équation d'Euler-Lagrange :

où f la fonction lagrangienne qui décrit le coût associé à chaque point du chemin et :
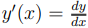
On cherche donc la fonction y(x) qui minimise sur le chemin l’action L(y) représenté par l’intégrale de la fonction lagrangienne f(y, y', x) sur l'intervalle [xA,xB] où y(xA) = y(xB) = Cste, y' est la dérivée de y par rapport à x. Autrement dit, on cherche la fonction y(x) qui minimise la longueur parcourue entre A et B :

Soit :

Or puisque f ne dépend pas de y, on a d’après l’equation d’Euler-Lagrange :

Où C est une constante appartenant à ℝ
Donc :



On peut donc en déduire la fonction affine d'une droite qui passe par A et B :

Dans cet exemple la réponse était évidente, mais l’approche variationnelle est très utile lorsque l’espace-temps est doté d’une métrique plus complexe dans le cadre de la théorie de la relativité par exemple.
Considérons un deuxième exemple plus concret pour illustrer le principe de moindre action :
Un objet part d’un point A1 à l’instant t1 et arrive au point A2 `a l’instant t2. Il existe une infinité de chemins entre ces deux points, pourtant l’objet en choisit un seul, la trajectoire physique:

Différents chemins qi(t) (i = 0, 1, 2, 3) en fonction du temps t. La trajectoire réelle q0 représentant un mouvement de chute libre dans le champ de pesanteur est représentée en traits pleins.
Plus généralement, cette fonction peut dépendre explicitement du temps. On définit donc l’action par:

où la fonction L(q(t), q˙(t), t) est appelée le Lagrangien du système. Rappelons que la fonction L dépend du temps explicitement, mais aussi implicitement à travers q(t) et ˙q(t).
Or la différentielle totale exacte de L est donnée par :

Donc la dérivée de L par rapport à t est :

Pour un chemin donné, tel que q(t1) et q(t2) sont fixés, S[q] prend une certaine valeur. D’après le principe de moindre action, la trajectoire physique est le chemin qui donne une valeur minimale à l’action. La trajectoire est donc donnée par l’équation d’Euler-Lagrange :

Plus généralement, le principe de moindre action implique que la dynamique d’une quantité physique (position d’une particule, valeur d’un champ,...) se déduit d’une unique grandeur, appelée action, qui doit être minimale pour représenter la réalité.
Comment écrire le Lagrangien d’un système ?
Considérons pour commencer une particule libre. L'équation de la dynamique pour une particule libre, c'est-à-dire une particule qui ne subit aucune force extérieure, est simplement donnée par la seconde loi de Newton : F = ma, où F est la force nette agissant sur la particule, m est sa masse et a est son accélération.
Pour une particule libre, la force nette est nulle, donc l'équation de la dynamique se réduit à : ma = 0. Cela signifie que l'accélération de la particule est nulle, c'est-à-dire que sa vitesse est constante, soit :

Or, le Lagrangien d’une particule libre est indépendant de la position q, car l’espace est homogène. En effet, en raisonnant à partir des symétries du système dans l'espace-temps. Par symétrie, le Lagrangien d’une particule libre (soumise à aucune force) ne peut pas dépendre explicitement de la position q ou du temps t, car cela violerait l'invariance de la physique par rapport aux translations de l'espace et du temps. De même, le Lagrangien ne peut pas dépendre de la direction de la vitesse de la particule, car cela violerait l'isotropie de l'espace. En effet, supposons que le Lagrangien dépend de la position. Si nous effectuons une translation de l'espace, c'est-à-dire que nous déplaçons tout le système physique de la même quantité dans une direction donnée, cela changerait la valeur du Lagrangien, car la position de la particule a changé. Cela contredirait l'invariance par translation de l'espace. C’est donc une fonction de la norme de la vitesse uniquement (qui peut a priori varier au cours du temps). A une dimension on a donc L = f( ˙q 2 ). Le principe de relativité de Galilée impose ensuite la forme du Lagrangien.
Par conséquent, l’équation d’Euler-Lagrange s'écrit :

En comparant avec l’´equation fondamentale de la dynamique précédente, on peut en déduire que :

où C est une constante. Soit, en intégrant :

où D est une constante or rappelons que le Lagrangien de la particule libre doit être indépendant de q car l’espace est homogène et étant également isotrope, le Lagrangien ne peut dépendre de la direction de sa vitesse mais uniquement de sa norme ˙q^2 (et non pas de ˙q) donc (à une constante près), on peut en déduire que :
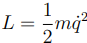
Dans le cas où le système serait soumis à une force conservative, il est raisonnable d’écrire le Lagrangien sous la forme:

où f est une fonction qui ne dépend que de la position.
Or retrouver l’équation fondamentale de la dynamique à l’aide de l’équation d’Euler-Lagrange impose f(q) = −U(q), où U est l’énergie potentielle d’intéraction. Soit (1) :

Ainsi, dans le cas où U = U(q), l’´energie potentielle ne dépend que de la coordonnée q, l’équation d’Euler-Lagrange impliquera donc :
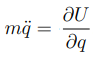
On écrira donc le Lagrangien comme:

où T est l’énergie cinétique et U l’énergie potentielle.
Un troisième exemple d'une particule libre en coordonnées polaires :
Il n’est bien sûr pas naturel d’étudier un mouvement rectiligne uniforme en coordonnées
polaires, mais cet exemple montre bien que le traitement d’un problème de mécanique à l’aide de coordonnées généralisées est indépendant du système de coordonnées choisi.
On a vu que le Lagrangien d’une particule libre s’écrit L = 1 / 2 mv2 , où v est la vitesse de la particule. Exprimons sa position puis sa vitesse en coordonnées polaires :


Soit:

Donc l'équation d’Euler-Lagrange pour les coordonnées q1 = r et q2 = θ impliquent :

A l’aide d’un changement de variables, il est possible de montrer que la trajectoire est une droite (en coordonnées polaires) et que le vecteur vitesse est constant (la deuxième équation montre la conservation du moment cinétique).
Considérons le nouvel exemple d'un pendule de longueur l décrit par l’angle θ :

L'énergie potentielle de pesanteur de la masse m est donnée par :

Son énergie cinétique est donnée par :

Or la relation entre la vitesse angulaire du pendule ω (rad·s^-1) et sa vitesse linéaire v de la masse m (m·s^-1) est donnée par∶

Donc :

Donc le Lagrangien du pendule est :

Et l’équation d’Euler-Lagrange implique :

On retrouve l’´equation du mouvement du pendule :

1.3. IDENTITÉ DE BELTRAMI
Nous allons démontrer ici une relation utile dans certaines situations. Il s'agit d'une relation appelée "identité de Beltrami" qui simplifie l'application de l'équation d'Euler-Lagrange dans certaines situations bien particulières.
Rappelons l'équation d'Euler-Lagrange:

Or rappelons la différentielle totale exacte du Lagrangien L (cf. section Calcul Différentiel et Intégral):

Que nous pouvons écrire sous la forme en divisant par dt de part & d'autre:

Soit :

Or multiplions par qi. de part & d'autre de l'équation d'E-L:

et injectons la relation antéprécédente dans la précédente:


Dans les conditions particulières (mais relativement fréquents en physique), que nous appelerons sur ce site la "condition de Beltrami", où:
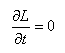
nous obtenons "l'identité de Beltrami":

Soit:

1.4. FORMALISME CANONIQUE
Le formalisme canonique n'introduit pas une nouvelle physique mais propose une nouvelle gamme d'outils pour étudier les phénomènes physiques. Son élément central, le "Hamiltonien", joue un grand rôle en physique. En effet, l'action est une grandeur mathématique qui décrit l'évolution d'un système physique au cours du temps. Elle est souvent utilisée en conjonction avec le principe de moindre action, également appelé principe de Hamilton, pour déterminer les équations du mouvement (champs) d'un système.
Comme dans le formalisme de Lagrange nous travaillerons avec des quantités comme l'énergie, T et V plutôt qu'avec des quantités vectorielles comme la force de Newton.
Dans le formalisme de Lagrange, la description d'un système mécanique à n degrés de liberté décrits par les coordonnées générales qi indépendantes (non contraintes) nous mène à n équations d'Euler-Lagrange:

qui sont des équations différentielles du 2ème ordre.
Dans le formalisme canonique (ou de Hamilton), un système mécanique à n degrés de liberté toujours décrits par des qi indépendants nous mènera à 2n équations du premier ordre (plus simple à résoudre).
Chez Lagrange nous comparons principalement des trajectoires et par conséquent les qi et les qi. sont tous indépendants. Chez Hamilton nous devrons d'abord apprendre à définir les "moments généralisés", notés pi, pour remplacer les coordonnées généralisées qi. et qi qui sont aussi tous indépendants.
1.5 TRANSFORMATION DE LEGENDRE
Cette transformation est souvent utilisée en thermodynamique où elle permet de relier entre eux les différents potentiels thermodynamiques. En mécanique ou en géométrie elle permet de définir le hamiltonien à partir du lagrangien et inversement. Nous en allons en donner une description simplifiée mais suffisante.
Soit une fonction f(u,v) où u,v sont les deux variables indépendantes dont dépend f.
Soit :

La transformation de Legendre permet de définir une fonction g(u,w) qui peut remplacer f(u,v) tel que :

Or

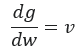
Et considérons maintenant la différentielle totale de f (cf. section de Calcul Différentiel Et Intégral):

Donc à partir de la définition de g nous pouvons en déduire que :

Soit:

1.6 HAMILTONIEN
Si le Lagrangien ne dépend pas explicitement du temps d'après la condition de Beltrami ( ∂L/∂t = 0) alors l'expression (3) :

est une constante du mouvement d'après la formule de Beltrami.
Dans le cas d’une force conservative (à une dimension), on voit que d'après (1) :

est une constante du mouvement, c’est-à-dire une variable dynamique (qui dépend des coordonnées généralisées) qui ne varie pas au cours du mouvement. On reconnaît bien sûr l’énergie du système 19. C’est donc parce que le Lagrangien ne dépend pas explicitement du temps que l’énergie est conservée au cours du mouvement. Une loi d’invariance (ici par rapport à une translation dans le temps) implique donc une loi de conservation (ici de l’énergie). Nous y reviendrons.
De plus, ce résultat suggère l’utilisation d’une autre fonction que le Lagrangien pour déduire les équations du mouvement. On définit le moment conjugué (ou impulsion généralisée) pi associé à la coordonnée qi par (4) :
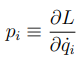
En général le moment conjugué est l’impulsion (d'après (1)) :
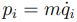
(cas des N particules ponctuelles), mais lorsque la coordonnée généralisée qi est un angle, son moment conjugué est un moment cinétique. Ainsi, dans le cas du pendule de longueur l décrit par l’angle θ. Le moment conjugué de θ est :
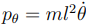
C’est-à-dire son moment cinétique.
Si le Lagrangien ne dépend pas explicitement de la variable qi on dit que cette variable est cyclique (∂L/∂qi = 0) et d’après les équations d’Euler-Lagrange son moment conjugué est une constante du mouvement (pi = ∂L/∂q˙i = cte) : A nouveau, une propriété d’invariance (ici par rapport à une translation dans l’espace) implique la loi de conservation d’une grandeur physique associée (ici l’impulsion). Nous avons déjà rencontré le cas d’une particule libre : le Lagrangien ne dépend pas de la position et l’impulsion p = mq˙ est conservée. Dans le cas d’un mouvement à force centrale (en coordonnées polaires à 2 d) le Lagrangien est par symétrie indépendant de l’angle θ :

L’impulsion généralisée pθ = ∂L/∂ ˙θ = mr²˙θ, c’est-à-dire le moment cinétique est donc conservé.
A partir de l’expression (3) et (4), définissons une nouvelle fonction appelée Hamiltonien (1834) et notée H :

Le Hamiltonien se confond avec l’énergie du système dans le cas de forces conservatives (et si ∂L/∂t = 0). On passe donc du Lagrangien au Hamiltonien par une transformation de Legendre.
Reste à trouver les équations du mouvement à partir de cette nouvelle fonction. Pour cela différencions H et utilisons l’équation d’Euler-Lagrange :

NB : L dépend de qi et qi. mais aussi de t d'où le différentiel par rapport à t
On voit que les variables naturelles du Hamiltonien sont les coordonnées qi et leurs moments conjugués pi. On en déduit les équations de Hamilton :

Comme les 3N équations du second ordre d’Euler-Lagrange, les 6N équations du premier ordre de Hamilton permettent d’exprimer les équations du mouvement. Elles ont également l’avantage d’être symétriques (au signe près) en qi et pi. De plus on peut en déduire du différentiel total exacte de l'hamiltonien que :

Un exemple s'avère indispensable à ce niveau d'avancement de l'étude du formalisme Lagrangien de l'Hamiltonien. Nous allons nous restreindre à un cas particulier d'une particule soumise à une force en une dimension:
Soit une particule de masse m se déplaçant en une dimension (disons x) et soumise à une force dérivant d'un potentiel tel que:

Nous savons que son lagrangien est:

Nous n'aurons qu'un seul moment (la quantité de mouvement), noté p, conjugué à x et défini par:
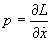
Equation que nous pouvons écrire sous une forme intégrant la définition de la quantité de mouvement:
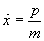
Nous pouvons noter en ce point que le moment p correspond à la composante x de la définition élémentaire p = mv (ce qui ne sera pas toujours aussi trivialement le cas).
Selon la définition de l'Hamiltonien vue plus haut, on écrit alors:

que nous pouvons noter sous la forme:
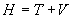
où T est donc l'énergie cinétique exprimée en fonction des moments.




