La relativité restreinte est une réussite remarquable d'un point de vue théorique aussi bien que d'un point de vue pratique en formant un continuum d'espace-temps où les grandeurs d'espace et de temps se voient donner la même dimension physique (celle d'une distance métrique pour rappel). Cependant, celle-ci s'applique aux repères euclidiens seulement et aux référentiels inertiels/Galiléens (à vitesse constante pour rappel). Il convient donc de généraliser l'ensemble de la mécanique d'abord en exprimant ses principes et ses résultats fondamentaux sous une forme généralisée indépendante du type de systèmes de coordonnées choisi (in extenso: du type d'espace) en faisant usage du calcul tensoriel et ensuite de prendre en compte les systèmes non inertiels.
1. POSTULATS ET PRINCIPES
Le principe d'équivalence (qui inclut le principe d'équivalence faible) affirme finalement que la force de Newton:
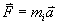
et celle de la gravitation selon la forme de la loi de Newton-Poisson:

sont équivalentes telles que la masse inerte mi égale la masse pesante mg et l'accélération a égale la pesanteur g et qu'il n'est pas possible de distinguer les deux:
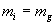
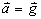
Dans un référentiel en chute libre, la force d'inertie d'entraînement est compensée par la force de pesanteur, ce qui crée l'impression d'apesanteur. Cela signifie que si vous êtes dans un objet en chute libre, vous ne ressentez pas la gravité tant que vous ne tenez pas compte des forces de frottement.
Lorsque nous allons considérer un corps en accélération, nous allons d'abord toujours assimiler celle-ci à l'accélération due à la chute dans un champ gravitationnel (selon le principe d'équivalence). Ensuite, nous allons supposer, et devrons le vérifier (démonstration plus bas) en retrouvant la loi de Newton, que l'accélération due à ce champ gravitationnel n'est pas due au champ lui-même mais à la géométrie de l'espace déformé par la présence de la masse (in extenso l'énergie) qui crée le champ gravitationnel. Ainsi, l'objet n'est plus en "chute libre" mais sera vu comme glissant sur la trame spatiale déformée pour acquérir ainsi son accélération.
En résumé, selon le principe d'équivalence, les effets de la gravité sont équivalents à ceux d'une accélération, et qu'il est possible de trouver un référentiel dans lequel les lois de la physique sont les mêmes que celles en l'absence de gravité.
L'enjeu est double:
1. Si le calcul tensoriel permet d'exprimer les lois de la mécanique classique et relativiste restreinte dans n'importe quel système de coordonnées, il est alors possible de voir comment le système de coordonnées (la métrique) agit sur l'expression des lois de l'Univers
2. Si l'expression tensorielle naturelle des lois de la mécanique fait apparaître le glissement (in extenso l'accélération) sur la trame spatiale suivant la métrique (locale) considérée, alors le pari est gagné et alors l'accélération peut être vue comme un effet dont la cause est purement géométrique.
Ainsi, l'extension de la relativité restreinte ne se fait plus en prenant en compte les systèmes non inertiels mais la géométrie du système.
Nous sommes donc amenés à énoncer le "principe d'équivalence d'Einstein" (PEE) tel que l'a fait Einstein: localement, toutes les lois de la physique sont les mêmes dans un champ gravitationnel et dans un référentiel uniformément accéléré.
Conséquence:
Si la masse (qui est équivalente à de l'énergie comme nous l'avons vu en relativité restreinte) d'un objet n'est pas différenciable que nous soyons dans un champ gravitationnel ou dans un référentiel uniformément accéléré c'est que tous les types d'énergie (énergie de cohésion nucléaire, énergie électrostatique, énergie gravifique propre de l'objet, etc.) de cet objet ne sont pas différenciables. Donc les lois de la relativité restreinte sont valables quel que soit le référentiel considéré!
Si les lois ne sont pas les mêmes, alors PEE est mis en défaut, donc in extenso PEF aussi et plus généralement le principe d'équivalence dans sa généralité mais ceci n'est encore jamais arrivé expérimentalement.
Étant donné qu'en relativité générale, le champ gravitationnel est censé être décrit par la métrique gµν (dont est munie la variété différentiable à 4 dimensions que constitue l'espace-temps), nous pouvons voir un référentiel localement inertiel comme un système de coordonnées de l'espace-temps dans lequel la métrique gµν devient plate (pseudo-Riemannienne):
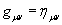
Lorsque la métrique n'est cependant pas plate, les coordonnées sont appelées "coordonnées normales de Riemann" et la métrique décrit alors un espace Riemannien (espace courbe) et dépend elle-même de manière non triviale des coordonnées du système.
NB : Principe d'équivalence faible (PEF): Pour tout événement de l'espace-temps dans un champ de gravitation arbitraire, nous pouvons choisir un référentiel dit "référentiel localement inertiel" tel que dans un voisinage de l'événement en question le mouvement libre de tous les corps (qui sont donc aussi dans le champ de gravité) soit rectiligne et uniforme tel qu'on puisse y appliquer les transformations de Lorentz
2. MÉTRIQUES
La métrique est ce qui permet de déterminer la distance entre deux points, elle représente en quelque sorte l'étalon infinitésimal d'un espace. En géométrie euclidienne la métrique est une constante, ce qui nous permet de créer des étalons de mesure universels. Bernhard Riemann, inventa une géométrie où la métrique peut varier d'un point à un autre de l'espace, ce qui lui permit de décrire des espaces courbes comme la
surface d'une sphère par exemple. La mesure de la distance ds entre deux points positionnés dans un espace à deux ou trois dimensions peut s'effectuer au moyen d'un grand nombre de système de coordonnées par "l'équation métrique" :

En relativité générale, l'idée est de rendre le modèle théorique indépendant du fond et donc le construire sous une forme covariante (ce que certains assimilent à un postulat sous le nom de "principe de covariance" : Par exemple, la vitesse de la lumière dans le vide est une constante qui est la même pour tous les observateurs, indépendamment de leur vitesse relative. Cette constance de la vitesse de la lumière est un exemple de covariance en action). Un excellent candidat pour ce type de démarche est donc d'utiliser le formalisme tensoriel. Raison pour laquelle l'équation de métrique en constitue aussi un des piliers.
Exemples :
1) Les coordonnées rectangulaires (dans ℝ³):

Si la distance au carré satisfait à cette relation alors nous sommes dans un espace plat.
2) En coordonnées polaires (dans ℝ²), la position du point M est définie par la distance r et l'angle θ :


Les deux coordonnées polaires r et θ peuvent être converties en coordonnées cartésiennes x et y en utilisant les fonctions trigonométriques sinus et cosinus :


D'où :

3) Les coordonnées cylindriques (dans ℝ³) pour lesquelles nous avons:

A remplacer dans :


Si la distance au carré satisfait à cette relation alors nous sommes dans un espace courbe (de type cylindrique) mais qui localement peut être plat. En réalité, pour avoir la métrique de la surface du cylindre et non pas simplement du plan exprimé en
coordonnées cylindriques, il faudra prendre la métrique suivante:

4) Les coordonnées sphériques (dans ℝ³) pour lesquelles nous avons:

Démonstration :
En effet, la position du point P est définie par le rayon de la sphère ρ (au lieu de r) et par les angles θ (colatitude) et φ (longitude) telle que :


La relation entre coordonnées cartésiennes and sphériques se déduit de la figure. Si l'on considére les triangles OPQ et OPP’, on a : z = ρ cos Φ, r = ρ sin Φ or x = r cos θ, y = r sin θ donc :
x = ρ sin Φ cos θ
y = ρ sin Φ sin θ
z = ρ cos Φ
Nous obtenons alors :

Or petit rappel préalable:

Donc:

Après une première série de mise en commun et de simplifications élémentaires des termes identiques, nous obtenons:

Si la distance au carré satisfait à cette relation alors nous sommes dans un espace courbe (de type sphérique) mais qui localement peut être plat. En réalité, pour avoir la métrique de la surface de la sphère et non pas simplement du plan exprimé en coordonnées sphériques, il faudra prendre la métrique suivante (r constant donc dr = 0 pour se situer à la surface de la sphère à r constant) :

Nous cherchons à définir à partir de ces relations, un modèle mathématique qui en concordance avec l'hypothèse d'Einstein, exprime les propriétés géométriques d'espaces donnés.
Nous allons d'abord changer d'écriture tout simplement. Au lieu d'utiliser les symboles x,y,z,θ,φ,r nous allons écrire x¹,x²,x³.... Attention! Les chiffres en suffixes ne sont pas des puissances. Ce sont des valeurs muettes qui sont là uniquement pour symboliser la x-ème coordonnée d'un repère donné.
Écrivons maintenant à nouveau nos équations métriques avec cette nouvelle notation en considérant qu'il ne s'agit que d'exemples particuliers qui n'ont pas nécessairement un sens physique pertinent :
- Coordonnées rectangulaires:

- Coordonnées polaires:

- Coordonnées cylindriques:

- Coordonnées sphériques:

Maintenant rappelons encore une fois que le "tenseur métrique" (nommé ainsi car il étalonne l'espace-temps) noté:

intervient dans l'équation métrique de la manière suivante:

et remarquez que les composantes de la matrice sont sans dimensions aussi.
Ce modèle mathématique qui est un tenseur contient donc les paramètres de la courbure (nous disons parfois aussi de la "contrainte" ou de la "tension") dans lequel un espace se trouve. Mais alors que contient le tenseur métrique d'espace-temps pour un espace euclidien plat?
Selon la convention d'écriture de sommation d'Einstein par exemple, pour m=n=2, nous avons:

Donc si nous revenons à notre tenseur pour l'espace euclidien plat, nous savons déjà que m et n vont de 1 à 3 et que nous avons dans notre tenseur gmn = 0 pour m≠n et gmn = 1 pour m=n (tenseur symétrique). Donc:

Soit :

Ce résultat est remarquable, car le tenseur métrique va donc nous permettre de définir les propriétés d'un espace à partir d'un simple modèle mathématique facilement manipulable formellement.
En coordonnées polaires le tenseur gmn s'écrit:

En effet,

En coordonnées cylindriques :

En coordonnées sphériques :

En relativité restreinte, nous avons vu que les notions d'espace et de temps étaient implicitement liées. Donc pour étudier la physique (cela intéresse peu le mathématicien), nous avons besoin d'ajouter à notre tenseur métrique la composante du temps pour obtenir ce que nous appelons le "tenseur métrique d'espace-temps".
Pour déterminer l'écriture de ce tenseur, nous allons nous placer dans un premier temps dans un espace de Minkowski où nous avions rappelons-le :

qui est donc l'intervalle infinitésimal d'espace-temps entre deux événements infiniment voisins. Ainsi, en posant:

Nous avons:

avec la "signature":

NB: Pour tous les tenseurs métriques que nous avons déterminés avant, si nous les exprimons dans l'espace-temps (donc en rajoutant le temps), les composantes spatiales ont toutes un signe négatif.
2.1. CRITÈRE DE SCHILD
Nous verrons que la gravitation telle qu'elle est formulée en mécanique newtonienne est entièrement descriptible à partir d'une formulation de courbure de l'espace-temps.
Imaginons d'abord une tour d'une très grande hauteur h construite à la surface de la Terre. Un homme A se trouve au pied de la tour, et envoie un signal de pulsation ωA à son collègue B situé en haut de la tour. Il se trouve, et nous allons de suite le démontrer, que la pulsation de l'onde ωB reçue par B diffère de ωA selon:
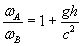
D'où:

Ce décalage des pulsations (respectivement des fréquences) dans un champ gravitationnel est ce que nous appelons "l'effet Einstein", ou encore "redshift gravitationnel".
NB : En relativité générale, le redshift gravitationnel est un phénomène dans lequel la lumière émise par un objet dans un champ gravitationnel intense (comme celui d'une étoile ou d'un objet hypermassif) est décalée vers le rouge, c'est-à-dire qu'elle a une fréquence plus basse et une longueur d'onde plus grande que si elle était émise dans un champ gravitationnel plus faible.
L'effet Einstein est un exemple de redshift gravitationnel, dans lequel la lumière est décalée vers le rouge en traversant un champ gravitationnel intense. Plus précisément, il s'agit du décalage vers le rouge d'une onde électromagnétique émise par un objet qui se déplace dans un champ gravitationnel, observé depuis un observateur en dehors de ce champ gravitationnel.
Lorsque la lumière se déplace dans l'univers en expansion, elle doit traverser des régions où l'espace est en train de s'étendre. Comme l'espace s'étend, la longueur d'onde de la lumière s'allonge également, ce qui entraîne un décalage vers le rouge de la lumière. Ce décalage vers le rouge est un indicateur important de la distance de l'objet observé, et il est utilisé pour mesurer les distances dans l'univers.
Nous allons démontrer cette relation à l'aide d'arguments classiques et connus maintenant.
Un corps matériel envoyé du sol vers le ciel doit lutter contre la force de gravitation qui l'attire vers le bas. Il perdra donc une certaine quantité d'énergie, équivalant à l'énergie potentielle gravitationnelle gagnée durant le trajet. L'énergie Ea du corps au niveau du sol est donc son énergie de masse à laquelle s'ajoute l'énergie potentielle à la hauteur de la tour:

L'énergie de ce corps une fois arrivé en haut de la tour est simplement son énergie de masse (L'énergie potentielle étant convertie):
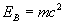
car il a dû dépenser la quantité d'énergie mgh durant le trajet. Le rapport des énergies est alors:

Ce rapport étant indépendant de la masse, on peut prendre la limite m->0 afin d'avoir la relation pour le photon. Nous obtenons alors:

NB : On rappelle la relation de Planck-Einstein (ou simplement relation de Planck) entre l'énergie E (en J) transportée par un photon et sa fréquence f (en Hz) : E = h f.
ce qui implique:
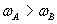
Nous allons maintenant étudier ce phénomène dans le cadre de l'espace-temps de Minkowski. Nous verrons apparaître une contradiction, ce qui motivera le passage vers un espace-temps courbe: c'est l'argument en faveur d'une géométrie courbe qui a été utilisé par Schild.
Nous retrouvons plus souvent cette relation sous la forme ci-dessous dans la littérature en utilisant les relations entre pulsation et fréquence et la force de gravitation de Newton pour expliciter g et en posant h comme valant 1:

Nous voyons dans tous les cas que fA > fB puisque le terme de droite est positif et non nul. Cela signifie simplement que l'onde électromagnétique en analogie au spectre des couleurs se décalera vers le rouge pour l'observateur A qui la recevra de B (fréquence plus basse = redshift, fréquence plus haute = blueshift). Ainsi, l'effet Einstein est bien un redshift gravitationnel traduisant simplement que le temps s'écoule effectivement moins vite dans un champ gravitationnel.
3. ÉQUATIONS DU MOUVEMENT
Nous allons démontrer ici que l'équation du mouvement d'une particule libre est constante le long de sa ligne d'Univers en nous limitant d'abord au cas d'un espace plat (de type espace de Minkowski). Après quoi, nous généraliserons ce résultat à tout type d'espace en utilisant un développement simple, pour montrer de manière assez évidente que l'équation du mouvement est indépendante de la masse et suit la courbure de l'espace. Enfin, nous présenterons une deuxième démonstration dans tout type d'espace en utilisant le principe variationnel.
Commençons donc par démontrer l'équation du mouvement d'une particule libre dans un espace plat.
En relativité, nous voulons que les équations du mouvement aient la même forme dans tous les référentiels inertiels. Pour cela, il faut que l'action S soit donc invariante par rapport aux transformations de Lorentz. Guidés par ce principe, essayons d'obtenir l'action d'une particule libre.
Supposons que l'action soit dans le référentiel O':

Or rappelons la contraction de Lorentz vu dans la section relative à la relativité restreinte:

Donc dans le référentiel O, nous pouvons écrire "l'action invariante de Lorentz":

Donc selon notre hypothèse initiale, nous avons pour le lagrangien relativiste (en l'absence du champ de potentiel puisque le système est "libre"):

Maintenant, montrons quelque chose d'intéressant. Rappelons que pour l'espace-temps de Minkowski, nous avons obtenu:

En nous restreignant à une seule dimension spatiale, nous obtenons comme relation:

Si nous posons:
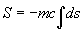
Nous obtenons :

nous retrouvons donc la même action à partir d'une forme plus générale (pure) de l'action qui est:
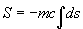
Dans un espace sans champ de potentiel, nous savons que le lagrangien se réduit à la simple expression de l'énergie cinétique tel que:

Si nous souhaitons généraliser cette relation pour qu'elle soit valable dans n'importe quel type d'espace (courbe ou plat), il nous faut introduire les coordonnées curvilignes telles que nous les avons étudiées en calcul tensoriel.
Dans un premier temps, cela donne:
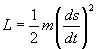
où rappelons-le ds est l'abscisse curviligne de la trajectoire.
Et nous savons qu'en calcul tensoriel :

Cette dernière relation s'écrit dans le contexte de la mécanique relativiste de manière plus standard:

t étant un paramètre qui correspond en mécanique au temps propre de la particule et qui dans la littérature spécialisée est souvent noté τ.
Avant de nous intéresser aux espaces courbes décrits par la métrique gij (ce que nous ferons lors de notre démonstration du lagrangien libre généralisé), restreignons-nous à l'espace euclidien avec la métrique (ce sera un bon exercice pour bien comprendre) donnée par la matrice de Minkowski :

que nous noterons pour la différencier des autres (car plus souvent utilisée). Nous avons finalement ηₐᵦ dans l'espace euclidien:

Maintenant, appliquons le principe variationnel:

La variation de ds peut être trouvée plus simplement à partir de la variation de ds² :

On trouve:

Le facteur "2" provient du fait que par symétrie de l'espace euclidien, les variations de dxα et dxβ sont égales.
En simplifiant un peu, nous obtenons:

Ce qui est équivalent à:

Nous pouvons maintenant revenir à l'action:

Soit:

Nous avons donc deux intégrales qu'il va être un peu plus simple d'analyser. La première intégrale:

Donne simplement une expression évaluée aux extrémités temporelles t1 et t2. Or dès lors, comme les valeurs xα de sont parfaitement connues aux extrémités temporelles, le variationnel δxα est nul aux deux bornes et cette intégrale est nulle (Voir section sur le calcul différentiel).
Il ne nous reste alors plus que l'intégrale:

Donc pour que le principe variationnel δS = 0 soit respecté, il faut que nous ayons (1):

Or, nous pouvons réécrire une partie de cette expression. Effectivement, nous avons (2):

Or nous avons démontré plus haut que pour une dimension :

Donc (3)

Or :

Donc (4) :

Alors (3) + (4) donne (5) :

Maintenant, sachant que le cheminement qui nous amenait à définir le quadrivecteur d'énergie impulsion (6):

Donc d'après (1) (2) et (5), nous pouvons en déduire que ce qui annule le variationnel de l'intégrale d'action peut s'écrire:
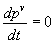
Nous retrouvons donc l'équation de conservation de la quantité de mouvement (conservation de l'impulsion) que nous appelons dans le cadre de la relativité générale "équation du mouvement". Cette forme de l'équation du mouvement semble dépendante de la masse mais en développant un peu, nous verrons qu'il n'en est rien.
En multipliant cette relation par ηᵤᵥ nous pouvons aussi écrire:
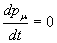
Mais nous pouvons aussi écrire:

Donc:

Une forme plus importante encore de l'équation du mouvement peut être obtenue d'après (5) et (6) :

Donc:
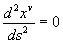
Rappelons qu'en relativité restreinte, la variable "x" représente la distance parcourue par la particule, tandis que la variable "s" représente le temps propre de la particule (c'est-à-dire le temps qui s'écoule pour un observateur attaché à la particule). Cette relation traduit donc la forme "sans masse" de l'équation du mouvement dans un espace-temps de Minkowski. Autrement dit, il existe donc un système de coordonnées en chute libre dans lequel le mouvement de la particule est celui d'un déplacement uniforme dans l'espace-temps (Vitesse constante)
Il sera très intéressant de la comparer avec l'équation du mouvement dans un espace courbe que nous verrons plus loin (appelée "équation des géodésiques").
Nous pouvons maintenant montrer que l'équation du mouvement, au même titre que l'équation des géodésiques que nous verrons de suite après, est invariante par transformation de Lorentz:

Maintenant, voyons une forme plus générale de l'équation du mouvement pour tout type d'espace. L'objectif ici est de mettre en évidence, et ce en quelques lignes de calculs, que le mouvement suivi par une particule libre est indépendant de sa masse.
Revenons à cette équation :

ce qui donne pour le lagrangien généralisé d'une particule libre avec:

l'expression générale de l'énergie cinétique ou le lagrangien géodésique (Voir section Mécanique lagrangienne):

où t est le temps propre de la particule qui est invariant.
NB: Le temps propre est une sorte d'horloge imaginaire qui voyage sur la particule et quels que soient les observateurs qui regardent l'horloge, ils seront mathématiquement d'accord sur la valeur de l'intervalle de temps entre deux "TIC" de l'horloge.
On peut déduire du lagrangien géodésique la quantité de mouvement :

L'élimination du facteur 1/2 du Lagrangien provient de la symétrie du tenseur métrique. Si ce dernier n'est pas symétrique, nous pouvons toujours le caractériser par un tenseur qui l'est.
3.1. ÉQUATION DES GÉODÉSIQUES
Rappelons le principe d'équivalence d'Einstein relatif à un référentiel inertiel en chute libre :
"Dans un champ de gravitation, il est toujours possible, en tout point de l'espace-temps, de choisir un système de coordonnées localement inertiel tel que, dans une région suffisamment petite, les lois de la physique soient identiques à celles en l'absence de gravité."
Dans ce référentiel en chute libre, la force d'inertie d'entrainement d'un corps en chute libre annule la force de gravitation, ce qui signifie que l'objet n'est soumis à aucune force (état d'apesanteur). Donc le référentiel inertiel est référentiel de base pour étudier les objets en intéraction (Référentiel dit de la relativité restreinte) avant de les étudier dans un second référentiel galiléen dit "de laboratoire" où ces objets sont soumis à l'effet de la gravitation. Et, ce dernier est un référentiel qui est en réalité accéléré vers le haut (a = -g) par rapport au référentiel inertiel naturel (Imaginez que "le sol sur Terre vous accélére vers le haut").
Un référentiel inertiel est structuré par la métrique de Minkowski qui est une formulation mathématique de l'espace-temps plat dans la théorie de la relativité restreinte. Elle décrit la géométrie de l'espace-temps dans les régions où il n'y a pas de gravité.
L'équation de mouvement d'un objet soumis à aucune force gravitationnelle est donnée par ce qu'on appelle la géodésique. Une géodésique est la trajectoire suivie par un objet en l'absence de forces extérieures. Dans la métrique de Minkowski, les géodésiques correspondent à des lignes droites à vitesse constante (référentiel inertiel en chute libre).
1) Plaçons nous donc dans ce référentiel inertiel et définissons les coordonnées d'un point masse dans ce référentiel:

Ce corps n'étant soumis à aucune force (vitesse constante), on en déduit que:


où "τ" correspond à la métrique ou l'intervalle dans cet espace qu'on pourrait également noter "s" et il faut savoir que cette métrique est invariante quelque soit le référentiel.
2) Nous allons maintenant effectuer une transformation de coordonnées dans un nouveau référentiel galiléen de laboratoire "accéléré vers le haut" par rapport au référentiel inertiel précédent :

Or chaque coordonnées du nouveau référentiel galiléen dépénd des coordonnées du référentiel inertiel et vice et versa:


Et il faut se rappeler que ξ dépend de τ :

Donc chaque paramètre de ξ dans le nouveau référentiel dépend également de τ, nous pouvons donc en déduire que :

Que l'on peut écrire par sommation des indices répétés:


Or nous souhaitons dériver une seconde fois cette expression pour en déduire l'équation des géodésiques :

Donc :

Même opération appliquée que précédemment:


Or pour avoir une sommation sur les indices répétés :




Or pour β≠µ, les dérivées partielles d'une coordonnée par rapport à une autre coordonnée du même référentiel de coordonnées est nulle (exemple ∂t/∂x=0) et pour β=µ, la dérivée partielle est égale à 1. Ce qui correspond au symbole de Kronecker :

L'expression donne alors :

Or si on remplace β par µ (β=µ) alors δβµ = δββ = 1 et d²xµ/dτ²=d²xβ/dτ²

On peut donc en déduire l'équation des géodésiques suivantes:

Ce qui nous permet d'introduire le symboles de Christoffel:

Que nous apprend cette équation des géodésiques ?
La dérivée seconde des coordonnées dans le référentiel galiléen "accéléré" n'est plus nulle mais égale à l'équivalent de forces d'inertie appliquées à la relativité générale (en l'occurence la gravité ici) :

En effet, si µ et ν sont des coordonnées d'espace alors leur dérivée pa rapport à τ corresponde à une vitesse
N'importe quel corps en mouvement dans le référentiel galiléen "accéléré" du laboratoire obéira à cette équation soumis à la force de la gravitation terrestre
La forme de cette équation nous renseigne sur les trajectoires les plus courtes ou les plus longues (extremums) sur une surface courbée (variété), plus précisémment les géodésiques correspondent aux chemins stationnaires dont les propriétés physiques restent constantes dans le temps (absence de forces extérieures appliquées)
On peut décrire la gravitation comme un effet purement géométrique lié aux géodésiques parcourues par les objets dans un espace-temps courbé (la manière dont l'espace-temps est courbée est décrite par les symboles de Christoffel). Une analogie serait de considérer que 2 objets parcourant de manière parallèle 2 trajectoires identiques, à la même vitesse depuis un point sur terre vers le nord, finiront par se croiser au pôle lié à la courbure terrestre. On peut analyser ce croisement soit par le fait qu'une force les a attiré (Analogie avec la mécanique newtonienne) ou à un effet purement géométrique lié à la courbure terrestre (Analogie avec la mécanique relativiste). La gravitation selon la relativité générale c'est donc une courbure de l'espace-temps amenant les objets en mouvement localement rectiligne à suivre ces géodésiques. La relativité générale nous permet donc de déterminer la courbure de l'espace-temps à partir de ce qui le compose (matière, énergie) puis de décrire la trajectoires des particules en mouvement à l'intérieur de cet espace-temps.
Les symboles de Christoffel sont calculés à partir de la métrique et de ses dérivées partielles et ils capturent l'information sur la courbure de l'espace-temps. Ils permettent de calculer comment les géodésiques sont affectées par la courbure de l'espace-temps.
4. TENSEURS METRIQUES
Nous allons nous intéresser aux tenseurs métriques et son lien avec les symboles de Christoffel déterminés précédemment.
Rappelons la métrique de Minkowski exprimée avec les coordonnées spatio-temporelles d'un corps en mouvement dans un référentiel inertiel:

On peut également l'écrire de cette manière où on peut noter une sommation sur les indices α et β:

où ηₐᵦ ne peut être qu'une matrice diagonale 4*4 sous cette forme :

En effet, pour les indices identiques α et β des termes dξα et dξβ de la métrique (α=β donc (dξ0)², (dξ1)², (dξ2)², (dξ3)²), nous obtenons les facteurs (1,-1,-1,-1) devant chaque coordonnée de la métrique, que l'on reporte donc dans les composantes diagonales η00, η11, η22, η33 de la matrice. Les termes croisés de la métrique d'indices α et β différents étant nuls impliquent que les composantes de la matrice d'indices différents soient nulles aussi.
Revenons à la forme de l'intervalle ou la métrique mais dans le nouveau référentiel galiléen accéléré représenté par les coordonnées:

Rappelons:

NB: µ étant un indice muet car répété dans la différentielle dξα, on peut le remplacer par n'importe quelle lettre grecque, et pour ne pas mélanger les indices lorsque nous remplaçerons dξα et dξβ dans la métrique, nous allons choisir ν comme second indice répété pour décrire la différentielle dξβ
Remplaçons ces 2 formes différentielles dans l'expression :

D'où on peut extraire le tenseur métrique:

Soit:

Le tenseur métrique est le noyau de la relativité car il détermine le potentiel gravitationnel de l'espace-temps entre 2 objets repérés par des coordonnées xµ et xν dans le même référentiel. permet à partir des coordonnées d'un objet
En effet, les coordonnées de 2 points de l'espace-temps ne sont pas suffisantes pour déterminer la distance qui les sépare. Par exemple, considérons 3 logements de numéros d'adresse respectifs 3, 4 et 15. Le logement numéro 4 n'est pas forcément plus proche du 3 que le numéro 15. Par ailleurs, la distance séparant le 3 du 4 est peut être 20 plus grande que celle qui sépare le 4 du 15 car il peut y avoir 10 stades de football séparant le 3 du 4 alors qu'il n'y a que 5 mètres de gazon séparant le 4 du 15. Par analogie avec la relativité, la distance entre deux points dans l'espace-temps courbé dépend de la courbure locale de l'espace-temps qui peut varier en fonction de la distribution de la matière et de l'énergie. Le tenseur métrique est donc l'objet mathématique permetant de passer des coordonnées de 2 objets à la distance qui les sépare car la présence d'un champ gravitationnel module l'intervalle entre ces objets incluant au passage le temps écoulé entre 2 évènements.
Comme les indices µ et ν sont muets et répétés, on peut les interchanger dans l'expression d'intervalle métrique, ce qui implique que le tenseur métrique g_µν est symétrique aussi (g_µν = g_νµ).
A présent, notons g^µν l'inverse de g_µν, ceci de part la relation suivante avec une sommation sur l'indice répété α (qui donne le symbole de Kronecker):

En effet, si on utilise la convention de sommation implicite sur les indices répétés, le produit de 2 matrices est donné par la relation suivante :

Nous avons démontré que:


NB : On avons remplacé α par λ
Nous allons à présent exprimer les symboles de Christoffel en fonction du tenseur métrique gµν. Pour celà, on peut voir qu'en dérivant gµν par rapport à x, on fait intervenir une dérivée seconde de ξ qu'on pourra donc intégrer dans la seconde expression des symboles de Christoffel.
Quelques astuces préalables pour simplifier les calculs :
- le tenseur métrique est symétrique donc g_µν = g_νµ
- Je souhaite remplacer ν par α mais pour celà, il faut déjà que je remplace l'indice muet répété existant α par σ:


On applique la dérivée d'un produit (ησβ étant une constante pour rappel) :

On voit apparaître la dérivée partielle seconde attendue dans le second membre (2 fois) :

Or pour pouvoir intégrer l'expression des symboles de Christoffel dans cette relation, il faut appliquer cette transformation de part et d'autre pour isoler la dérivée partielle:

Pour faire intervenir une somme sur l'indice répété β:

Or on sait que :

Or comme nous l'avons déjà vu plus haut, si on remplace σ par λ (σ=λ) alors δσλ = δλλ = 1 et ∂ξσ/∂xβ = ∂ξλ/∂xβ donc:

On peut alors la remplacer dans l'expression ici en faisant attention à reformuler par analogie les indices correspondants dans la nouvelle expression :

NB : On ne remet pas β sur le symbole de Christoffel car c'est un indice muet de sommation dans le membre où on souhaite l'affecter donc on choisira une autre lettre ρ:

Même modification par analogie sur la seconde partie du second membre :

NB: On ne remet pas β sur le symbole de Christoffel car c'est un indice muet de sommation dans le membre où on souhaite l'affecter donc on choisira une autre lettre ρ.
D'où l'expression finale:

Or:

Donc la dérivation du tenseur métrique peut alors s'écrire de 3 manières différentes (les 2 dernières faisant intervenir de nouveaux indices en interchangeant ν µ et en remplaçant µ par α):



Ces 3 façons d'écrire cette dérivation nous permettent de pouvoir obtenir un résultat simplifié en additionnant les 2 premières moins la dernière :

Qui donne :


Puis par le rappel de cette opération donnant le symbole de Kronecker au premier membre :



Pour simplifier l'écriture, on peut utiliser cette notation :

Soit finalement:

Cette expression du symbole de Christoffel permet donc de mettre en relation la courbure de l'espace-temps induite par la force gravitationnelle et les dérivées spatiales du tenseur métrique.
Application de l'équation des géodésiques dans la limites des champs faibles:
Notons l'expression du symbole de Christoffel et l'équation des géodésiques de la manière suivante (Si ν=0 : coordonnée temporelle sinon c'est une coordonnée spatiale x,y,z) :

En relativité, on se place souvent dans un système d'unité où c=1 afin de pouvoir assimiler la métrique s au temps propre τ de l'observateur pour pouvoir alors exprimer la métrique de minkowski de la même manière pour un point masse immobile dans l'espace-temps :

Pour celà, le temps doit être exprimé en seconde et les unités de longueur deviennent une longueur parcourue par la lumière en une seconde qui s'expriment en seconde-lumière (équivalent à "année-lumière"). On peut ainsi exprimer la métrique ainsi:

Néanmoins, nous allons à présent considérer que le temps t exprimé jusqu'à maintenant sera le temps propre τ dans l'expression de la métrique afin de pouvoir l'exprimer ainsi :

L'équation des géodésiques sera exprimée alors ainsi :

Nous allons à présent démontrer que cette équation se ramène à l'équation du mouvement newtonienne lorsque les champs gravitationnels sont faibles et statiques (Relativité restreinte où g_µν est très proche de η_µν et indépendant du temps) et les vitesses sont faibles devant celles de la lumière v/c<<1 soit :


En intégrant ce tenseur métrique dans l'expression du symbole de Christoffel , on se rend compte que les dérivées partielles du tenseur métrique ne dépendent que de h_µν puisque η_µν est une constante ne dépendant ni des coordonnées spatiales ni de la coordonnée temporelle:

Ce qui donne :

On se rend compte que le produit de h^λσ par les dérivées partielles de h par rapport à µ,ν,σ va donner un développement limité d'ordre 2 au moins (en h^2, h^3...) dont le résultat va donc être très négligeable par rapport aux termes d'ordre 0 ou 1 qui nous intéressent, ce qui implique que h^λσ sera négligeable devant η^λσ:


Pour λ = 0 (coordonnée temporelle):


Et comme nous l'avons évoqué, le champ gravitationnel est statique donc la dérivée partielle du tenseur métrique par rapport au temps (indice 0) est nul:

Soit:

Pour λ = i (coordonnées spatiales i,j,k):


Donc:

Intégrons à présent ces résultats dans l'équation des géodésiques pour chaque cas :

Pour λ = 0 (coordonnée temporelle):
On sait que x^λ = x^0 = c t :

Or le produit suivant va générer une somme sur des indices répétés µ et ν de quantités d'ordre 0, 1 et 2:


Les quantités d'ordre 1 et 2 étant très négligeables, d'autant qu'elles sont basées sur une quantité déjà négligeable h_µν << η_µν, on ne gardera que les quantités d'ordre 0 où µ et ν sont égales à 0 à savoir les variables temporelles :

Or nous avons postulé que les champs gravitationnels sont faibles et statiques (à savoir qu'en relativité restreinte la dérivée du tenseur métrique g_µν est égale à h_µν et elle est indépendante du temps) :

Donc:

Ce qui implique que t est proportionnel à s soit :

Pour λ = i (coordonnées spatiales i,j,k):
On sait que ds = c dt donc:

Or comme plus haut, on allons conserver uniquement les quantités d'ordre 0 pour µ et ν qui sont égaux à 0:

et les champs gravitationnels sont statiques donc :


i étant un indice spatial prenant 1,2 ou 3, nous retrouvons donc une forme d'équivalence "Accélération - Force" qu'on peut noter sous forme de vecteurs:

Avec

Et le lien entre le potentiel gravitationnel et la composante temporelle du tenseur métrique:


NB:
Le gradient de φ ou du potentiel gravitationnel s'exprime par :

Le potentiel gravitationnel φ est assimilable à une vitesse au carré (c^2)
Sachant que h_µν << η_µν, on peut vérifier localement que pour la Terre, h_00 = (2φ/c^2) = (2*G*Mt)/(Rt*c^2) = 10^-9 << η_00 = 1 d'après l'expression connue du calcul du potentiel gravitationnel :


4.1 COURBURES ET TENSEUR
Les tenseurs sont des objets mathématiques issus de l'algèbre multilinéaire permettant de généraliser les scalaires et les vecteurs.
- Scalaire :
Considérons 2 systèmes de coordonnées dont l'un x'^µ correspond à la transformation du premier x^µ:

Le scalaire permet de passer un point d'un système de coordonnées S vers un nouveau système de coordoonnées S'.
En effet, si on souhaite passer un point M d'un système de coordonnées cartésiennes S : x^µ(x,y) vers un nouveau système de coordonnées polaires S' : x'^µ(r,θ), il faut opérer cette transformation :


- Vecteur :

On exprime les coordonnées du vecteur en fonction de r,θ dans le nouveau système de coordoonées mais on les exprime en plus en fonction de nouveaux vecteurs de base (ur,uθ)

Donc un scalaire est juste un nombre en tout point de l'espace alors qu'un vecteur est composé d'un nombre qui est sa longueur (norme) et une direction.
La loi de transformation d'un vecteur depuis un système de coordonnées x^µ vers un nouveau système de coordonnées x'^µ est donc plus compliquée que celle d'un scalaire et il en existe 2 sortes :
- Vecteurs contravariants dont nous dérivons les coordonnées du nouveau référentiel x'^µ par rapport à l'ancien x^v :

- Vecteurs covariants dont nous dérivons les coordonnées de l'ancien référentiel x^v par rapport au nouveau x'^µ :

Par exemple, considérons un vecteur de déplacement élémentaire qui relie 2 évènements distincts dans l'espace-temps séparés par (dt',dx',dy',dz') qu'on peut noter collectivement sous la forme dx'^µ alors:

Rappelons la différentielle totale exacte de f :
Sa variation par rapport à une de ses variables x,y,z fait intervenir une variation de toutes les variables implicites à l'intérieur. Donc une variation de la variable implicite t implique une variation de x,y,z par rapport à t uniquement (dérivée totale de x,y,z par rapport à t) et une dérivée partielle de f par rapport à chacun de ses paramètres x,y,z :

Soit le vecteur de déplacement élémentaire contravariant:


où µ peut prendre comme valeur 0,1,2,3
Nous allons démontrer à présent que la norme du vecteur V est donnée par la relation suivante :

En effet, considérons un repère non orthogonal (0xy) où le vecteur V possède des coordonnées covariantes et contravariantes:


En effet :


Or on obtient la même relation avec le 2ème triangle rectangle :

En sommant les 2 :

Soit :

Un tenseur de rang 2 peut manipuler 2 indices (1 indice de plus) :
- Covariant :

- Contravariant :

- Mixte :

Nous en déduisons donc qu'un tenseur de rang 2 est essentiellement une matrice ou un tableau à 2 indices qui représente une quantité physique dans un espace donné. Nous pouvons constater la transformation d'un tenseur de rang 2 d'un système de coordonnées à un autre système de coordonnées qui utilise les dérivées partielles (∂x^α)/(∂x'^μ) et (∂x^β)/(∂x'^ν) pour mesurer comment les coordonnées dans le nouveau système de coordonnées (x'^μ) sont liées aux coordonnées dans le système initial (x^α). Lorsqu'on applique cette transformation à un tenseur de rang 2 initial Tαβ, on obtient donc un nouveau tenseur de rang 2 Tμν' dans le nouveau système de coordonnées.
Pour réaliser une transformation de tenseur de sa définition contravariante à sa définition covariante et vice et versa (somme implicite sur v) :

Rappelons la définition du tenseur métrique (transformation des coordonnées d'un référentiel inertiel vers un référentiel quelconque comme galiléen) :

Que vaut à présent ce tenseur métrique dans un autre référentiel :




Ce qui démontre bien que g'μν est bien un tenseur et que les égalités tensorielles (entre tenseurs de même type) sont vraies dans tous les référentiels.
Propriétés des tenseurs : - Tout combinaisons linéaire de tenseurs est un tenseur
- Tout produit de tenseurs donne un tenseur de rang plus élevé. Par exemple, pour un tenseur e rang 2 Tμν, μ peut prendre 4 valeurs, ν peut prendre 4 valeurs soit une combinaison de 16 composantes que l'on multiplie par un autre tenseur de même rang donnera un tenseur de 16*16 = 256 composantes de rang 4. Donc Si vous multipliez deux tenseurs de rang 2, le nouveau tenseur aura un rang de 4. Pour déterminer le nombre de composantes de ce nouveau tenseur, il faut donc multiplier le nombre de composantes du premier tenseur par le nombre de composantes du deuxième tenseur.
- La contraction de 2 tenseurs donne un tenseur (Somme implicite par rapport à α sur les 4 valeurs possibles de chaque indice μ ν) :

Dérivée covariante
Nous savons que la dérivée d'une fonction scalaire se comporte comme un tenseur covariant de premier rang :

Considérons la dérivée par rapport à v d'un vecteur voyons comment cette grandeur se comporte par changement de coordonnées :



Or nous souhaitons exprimer cette relation en fonction d'un observateur situé dans le référentiel initial (non prime) soit avec une somme implicite sur les indices β :

Donc :






